a) Das Steigungsproblem

Zum Einstieg in die Steigungsproblematik betrachten wir einen freien Fall aus eine Höhe von 1000m.
Wir erstellen das zugehörige Weg-Zeit-Diagramm.

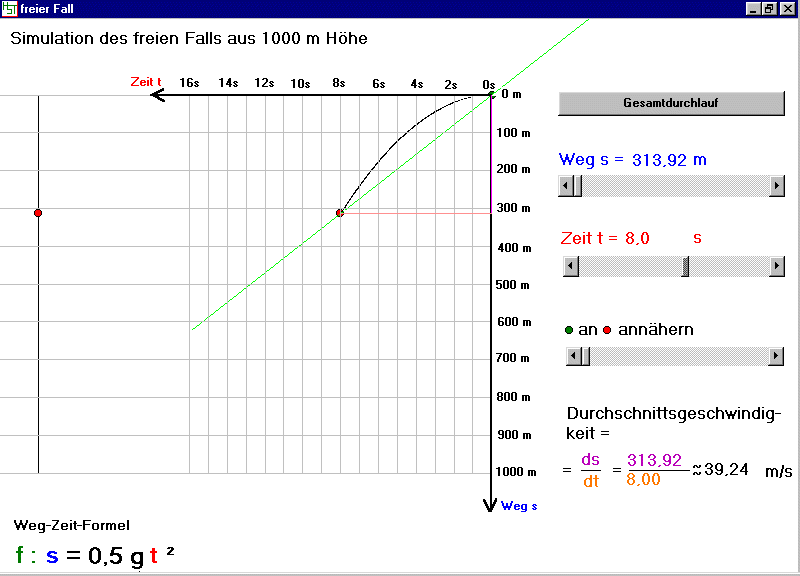
Wir erkennen, dass nach der Zeit t=8s ein Fallweg von s=313,92m zurückgelegt wurde. Die Durch-
schnittsgeschwindingkeit liegt somit bei v=39,24m/s (Anmerkung: Anfangsgeschwindigkeit vo=0m/s)

Betrachten wir den weiteren Verlauf:

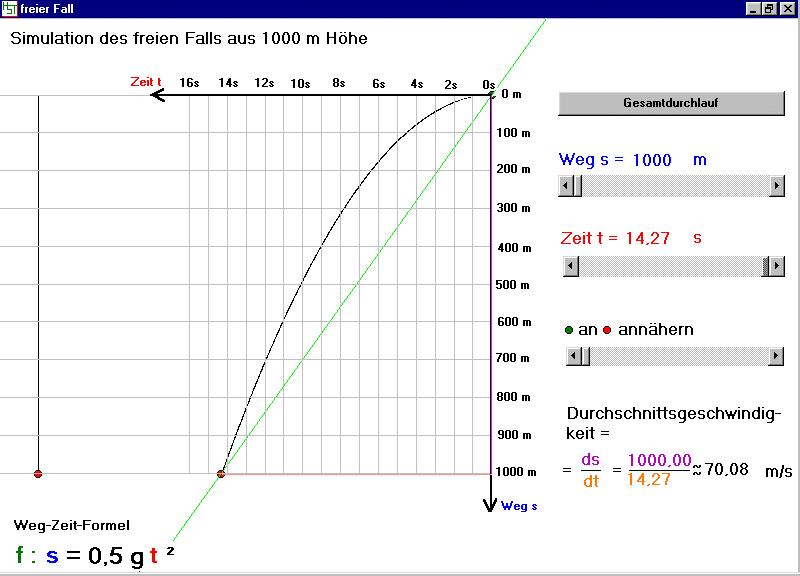
Die Fallhöhe von 1000m wird offensichtlich nach t=14,27s zurückgelegt. Die Durchschnittsgeschwin-
digkeit liegt somit bei v=70,08m/s.

Frage: Wie gross ist aber die End-/Momentangeschwindigkeit?

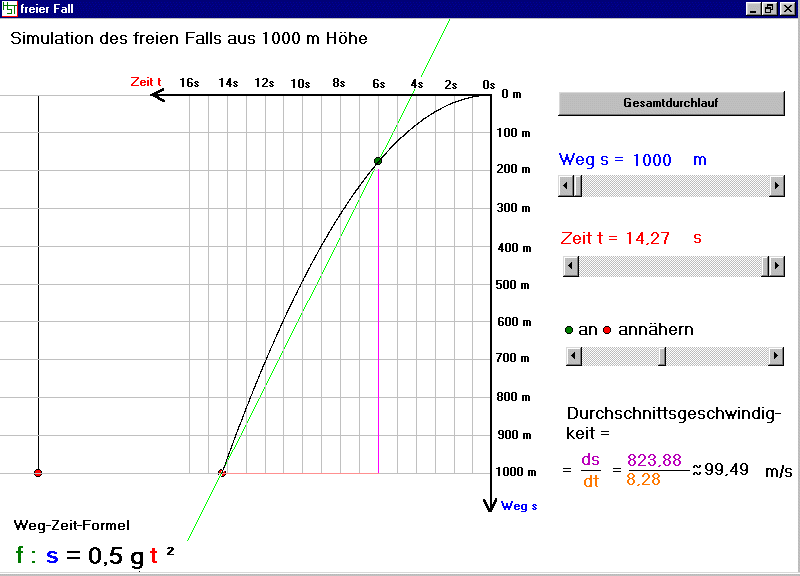
Vermutung: Wenn die Anfangsgeschwindigkeit mit 0m/s angenommen wird, die Durchnittsgeschwin-
digkeit bei 70m/s liegt, so ist anzunehmen, dass die Momentangeschwindigkeit bei 140m/s liegt!

vDurchschnitt=(vAnfang+vEnde)/2

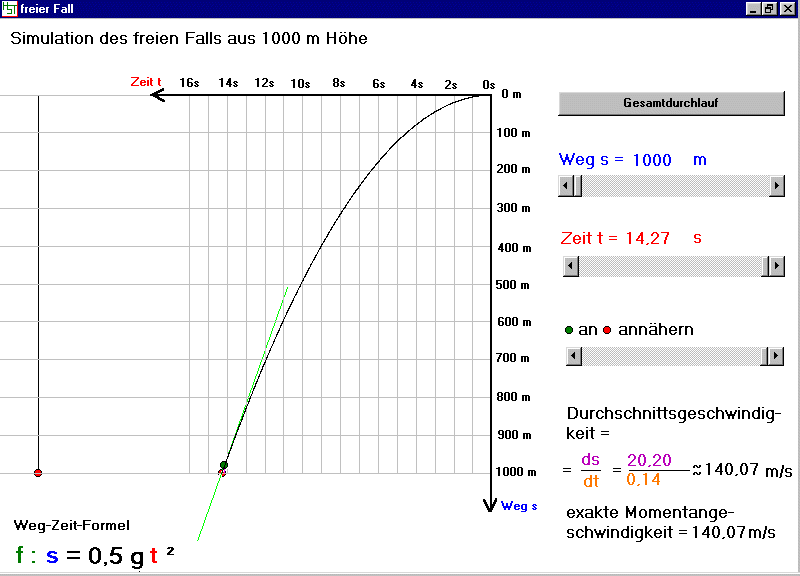
Wir erkennen, dass die Endgeschwindigkeit tatsächlich bei v=140,07m/s liegt.

Gehen wir aber auf die Darstellungen genauer ein.

Die Durchschnittsgeschwindigkeit innerhalb eines Zeitintervalls Dt= t2-t1 wird durch die Steigung
einer Sekante dargestellt.
Die Endgeschwindigkeit wird durch die Steigung der Tangente beschrieben. Da aber dann das
Zeit intervall Dt ->0 strebt, ist diese nicht ohne weiteres berechenbar.

Merke: Die Steigung einer nichtlinearen Kurve in einem Punkt P wird als
Steigung der Tangente in diesem Punkt definiert.

Die Berechnung dieser Tangentensteigung müssen wir gesondert untersuchen.